Los Múltiples Infinitos

Explorando el Infinito: Una mirada en sus Múltiples Facetas y Paradojas

El concepto de infinito ha sido objeto de fascinación y debate desde tiempos inmemoriales. Desde los antiguos filósofos griegos hasta los matemáticos contemporáneos, el infinito ha desafiado nuestras concepciones sobre el universo y ha dado lugar a un vasto campo de estudio en diversas disciplinas. En este extenso análisis, nos sumergiremos en el infinito desde múltiples perspectivas, explorando sus manifestaciones en matemáticas, filosofía y física, así como las paradojas que suscita y las teorías que intentan dar sentido a su insondable naturaleza.

El Infinito en Matemáticas:

El estudio del infinito en matemáticas ha sido profundamente influenciado por los trabajos de Georg Cantor, quien a finales del siglo XIX revolucionó nuestra comprensión del infinito al introducir la teoría de conjuntos. Cantor desarrolló el concepto de cardinalidad para comparar el tamaño de conjuntos infinitos, demostrando que hay diferentes tamaños de infinito. Por ejemplo, el conjunto de los números naturales (1, 2, 3,…) es infinito pero de un tamaño menor que el conjunto de todos los números reales entre 0 y 1. Esta revelación condujo a Cantor a formular la hipótesis del continuo, una de las conjeturas más famosas en la teoría de conjuntos que plantea la pregunta sobre la existencia de un conjunto cuya cardinalidad esté entre la de los números naturales y la de los números reales.

La jerarquía de infinitos descubierta por Cantor, denotada por los números cardinales ℵ₀, ℵ₁, ℵ₂, …, nos sumerge en un mundo de infinitos de diferentes «tamaños», desafiando nuestra intuición sobre la magnitud del infinito y planteando cuestiones profundas sobre la naturaleza de los conjuntos infinitos.

Paradojas del Infinito:

El infinito también nos confronta con una serie de paradojas que desafían nuestra comprensión intuitiva del mundo. Una de las más conocidas es la paradoja de Zenón de Elea, que se presenta en varias formas pero que es más famosa en la versión de Aquiles y la tortuga. Esta paradoja argumenta que, si dividimos una distancia finita en un número infinito de partes, cada una de las cuales es más pequeña que la anterior, entonces Aquiles nunca alcanzará a la tortuga. Esta paradoja, aunque resuelta con el advenimiento del cálculo infinitesimal, sigue siendo un recordatorio poderoso de las complejidades inherentes al concepto de infinito.

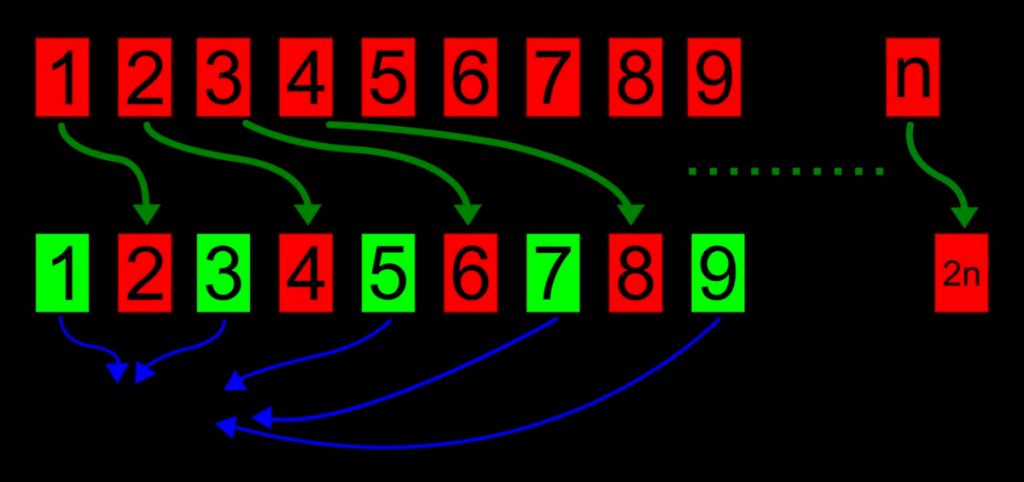
Otra paradoja intrigante es la paradoja del hotel de Hilbert, que desafía nuestra intuición sobre la cardinalidad de conjuntos infinitos. Imaginemos un hotel con un número infinito de habitaciones numeradas del 1 al infinito, todas ocupadas. Cuando llega un nuevo huésped, sorprendentemente podemos acomodarlo moviendo a cada huésped a la habitación siguiente. Esta paradoja ilustra cómo las propiedades únicas del infinito pueden conducir a conclusiones inesperadas y contraintuitivas.

El Infinito en Filosofía y Física:

En la filosofía, el infinito ha sido objeto de especulación desde la antigüedad, desde las ideas de Platón sobre el «Uno» hasta las reflexiones modernas sobre el infinito como un principio fundamental del universo. En la física, el infinito se encuentra en el centro de teorías como la relatividad general y la mecánica cuántica, donde las singularidades y los límites infinitos desafían nuestra comprensión del espacio, el tiempo y la materia.

La teoría del Big Bang, por ejemplo, plantea la pregunta de si el universo es finito o infinito en su extensión. Si el universo es infinito, ¿qué significa eso para nuestra comprensión del espacio y el tiempo? Por otro lado, en la mecánica cuántica, las teorías de cuerdas y la teoría de la gravitación cuántica buscan reconciliar el infinito de las singularidades gravitacionales con los principios de la mecánica cuántica, lo que plantea desafíos profundos y estimulantes para nuestra comprensión del universo a escalas extremadamente pequeñas y extremadamente grandes.

Conclusiones y Reflexiones:

En última instancia, el infinito sigue siendo uno de los conceptos más enigmáticos y evocadores en la exploración del universo y del conocimiento humano. Aunque nos enfrentamos a paradojas y desafíos en nuestra comprensión del infinito, estas mismas dificultades nos invitan a reflexionar más profundamente sobre la naturaleza de la realidad y el alcance de nuestro entendimiento. A medida que continuamos explorando las múltiples facetas del infinito, nos encontramos con nuevos enigmas y descubrimientos que enriquecen nuestra visión del universo y nuestro lugar en él.

Bibliografía:

1. Cantor, Georg. «Contribuciones a la Teoría de Conjuntos». 1874.
2. Dauben, Joseph W. «Georg Cantor: His Mathematics and Philosophy of the Infinite». 1979.
3. Enderton, Herbert B. «Elements of Set Theory». 1977.
4. Rucker, Rudy. «Infinity and the Mind: The Science and Philosophy of the Infinite». 1982.
5. Zenón de Elea. «Paradojas de Zenón». Siglo V a.C.

Este análisis superficial del infinito pretende ofrecer una panorámica completa de un tema tan vasto y complejo como es el infinito. Invito al lector a explorar más a fondo las obras citadas y a continuar indagando en las diversas dimensiones del infinito en todas sus formas y manifestaciones.